1  Models and meaning

The best way to start a data analysis project is to set clear goals. This chapter explores four of the main objectives that data analysts pursue when they fit statistical models or deploy machine learning algorithms: model description, data description, causal inference, and out-of-sample prediction.

To achieve these goals, it is crucial to articulate a well-defined research questions, and to explicitly specify the statistical quantities—the estimands—that can shed light on these questions. Ideally, estimands should be expressed in the simplest form possible, on a scale that feels intuitive to stakeholders, colleagues, and domain experts.

This chapter concludes by discussing some of the challenges that arise when trying to make sense of complex models. In many cases, the parameters of these models do not directly align with the estimands that can answer our question. Thus, we often need to transform parameter estimates into a form that our audience will readily understand.

1.1 Why fit a model?

The first challenge that all researchers must take on is to transparently state what they hope to achieve with an analysis. Below, we survey four of the goals that we can pursue: model description, data description, causal inference, and out-of-sample prediction.

1.1.1 Model description

The primary aim of model description is to understand how a fitted model behaves under different conditions. Here, the focus is set on the internal workings of the model itself, rather than on making predictions or inferences about the sample or population. We peek inside the “black-box” to audit, debug, or test how the model reacts to different inputs.

Model description aligns closely with the concepts of “interpretability,” “explainability,” and “transparency” in machine learning. It is an important activity, as it can provide some measure of reassurance that a fitted model works as intended, and is suitable for deployment.

To describe a fitted model’s behavior, the analyst might compute model-based predictions, that is, the expected value of the outcome variable for different subgroups of the sample (Chapter 5). For example, a real estate analyst may check if their fitted model yields reasonable expectations about home prices in different markets, and go back to the drawing board if those expectations are unrealistic.

In a different context, the analyst may conduct a counterfactual analysis to see how a model’s predictions change when we alter the values of some predictors (Chapter 6). For instance, a financial analyst may wish to guard against algorithmic discrimination by comparing what their model says about the default risk of borrowers from different ethnic backgrounds, when we hold other predictors constant.

1.1.2 Data description

Data description involves using statistical or machine learning models as tools to describe a sample, or to draw descriptive inference about a population. The objective here is to explore and understand the characteristics of the data, often by summarizing their (potentially joint) distribution. Descriptive and exploratory data analysis can help analysts uncover new patterns, trends, and relationships (Tukey 1977). It can stimulate the development of theory, or raise new research questions.

Data description is arguably more demanding than model description, because it imposes additional assumptions. Indeed, if the sample used to fit a model is not representative of the target population, or if the estimator is biased, descriptive inference may be misleading.

To describe their data, an analyst might use a statistical model to compute the expected value of an outcome for different subgroups of the data (Chapter 5). For example, a researcher could use this approach to estimate the expected forest coverage in the Côte Nord or Cantons de l’Est regions of Québec.

1.1.3 Causal inference

In causal inference our goal is to estimate the effect of an intervention (a.k.a., treatment, explanator, or predictor) on some outcome. This is a fundamental activity in all fields where understanding the consequences of a phenomenon helps us make informed decisions or policy recommendations.

Causal inference is one of the most ambitious and challenging tasks in data analysis. It typically requires careful experimental design, or statistical models that can adjust for all confounders in observational data. Several theoretical frameworks have been developed to help us understand the assumptions required to make credible claims about causality. Here, we briefly highlight two of the most important.

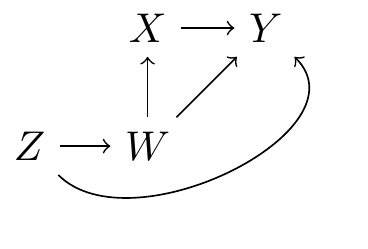
The structural causal models approach, developed by Judea Pearl and colleagues, encodes causal relationships as a set of equations that describe how variables influence each other. These equations can be represented visually by a directed acyclic graph (DAG), where nodes correspond to variables and arrows to causal effects. Consider Figure 1.1, which shows the causal relationships between a treatment \(X\), an outcome \(Y\), and two confounding variables \(Z\) and \(W\). Graphs like this one help us visualize the theorized data generating process, and communicate our assumptions transparently. By analyzing a DAG, we can also learn if a given statistical model fulfills the conditions required to identify a causal effect in a given context.1

Figure 1.1: Example of a Directed Acyclic Graph

Another influential theoretical approach to causality is the potential outcomes framework, or Neyman-Rubin Causal Model. In this tradition, we conceptualize causal effects as comparisons between potential outcomes: what would happen to the same individual under different treatment conditions? For each observation in a study, there are two potential outcomes. First, we ask what would happen if unit \(i\) received the treatment? Then, we ask what would happen if unit \(i\) were part of the control group? Finally, we define the causal effect as the difference between those two potential outcomes. Since only one potential outcome can ever be observed—a given unit cannot be part of both the treatment and control groups simultaneously—unit-level causal effects are unobservable.2 This inconvenient fact is often dubbed the “fundamental problem of causal inference.”

The literature on causality is vast, and a thorough discussion of Structural Causal Models or the Neyman-Rubin Model lies outside the scope of this book.3 Nevertheless, it is useful to reflect on the language that data analysts use when discussing empirical results drawn from observational data, or when conditions for causal identification are not satisfied.

When the DAG or potential outcomes suggest that a research design is imperfect, analysts will often revise their text to remove all causal language, and they will choose to use weaker associational terms instead. For instance, peer reviewers at scientific journals often recommend striking out words like “cause”, “affect”, “influence”, or “increases” from all observational studies, unless the research design clearly supports a causal interpretation. Researchers are encouraged to use terms like “link” or “association” instead.

In a provocative commentary, the epidemiologist Miguel Hernán (2018) fights back against this practice, and against the use of “causal euphemisms.” He points out that many researchers are fundamentally interested in understanding the effects of a cause, and that pretending otherwise is futile. Consider the large number of published studies on the “association between daily alcohol intake and risk of all-cause mortality” (Zhao et al. 2023). The research question that motivates this work is fundamentally causal: readers hope to learn how much longer they might live if they stopped drinking, and policy makers wish to know if discouraging alcohol intake would be good for public health. We do not care about mere association; we care about consequences!

As Hernán points out, changing a few adjectives in a paper does not fundamentally change the research question, and it does not absolve us of the responsibility to justify our assumptions. In fact, avoiding causal language may introduce ambiguity about a researcher’s goals, and could hinder scientific progress.

What are we to do? One way out of this conundrum is transparency. Researchers can candidly state: “I am interested in the causal effect of \(X\) on \(Y\), but my research design and data are limited, so I cannot make strong causal claims.” When both the goals of an analysis and the violations of its assumptions are laid out clearly, readers can interpret (and discount) the results appropriately.

Part II of this book presents two broad classes of estimands which can be used to characterize either the “association” between two variables, or the “effect” of one variable on another (Chapters 6 and 7). When describing those quantities, we will not shy away from using causal words like “increase,” “change,” or “affect.” However, analysts should be mindful that when conditions for causal identification are violated, they have a duty to signal those violations explicitly and clearly to their audience.

1.1.4 Out-of-sample prediction

Out-of-sample prediction and forecasting aim to predict future or unseen data points based on a model fit on existing data. This is particularly challenging due to the need to ensure that our model does not overfit the data and generalizes well.4 Furthermore, out-of-sample prediction imposes additional requirements on the stability of the data distribution, and on the absence of changes in exogenous factors between the training sample and the target data.

Out-of-sample prediction is not the main focus of this book, but Section 14.4 presents a case study on conformal prediction, a flexible strategy to make predictions and build intervals that will cover a specified proportion of out-of-sample observations.

1.2 What is your estimand?

Once the overarching goal of an analysis is posed, the next step is to rigorously define the specific empirical quantity that would shed light on our research question. In their article What is your estimand?, Lundberg, Johnson, and Stewart (2021) enjoin scientists to be clearer about this quantity:

“In every quantitative paper we read, every quantitative talk we attend, and every quantitative article we write, we should all ask one question: what is the estimand? The estimand is the object of inquiry—it is the precise quantity about which we marshal data to draw an inference.”

This injunction is sensible, yet many of us conduct statistical tests without explicitly defining the quantity of interest, and without explaining exactly how this quantity answers the research question. This failure to define our estimands impedes communication between researchers and audiences, and it can lead us all astray.

To see how, imagine a dataset produced by the data generating process in Figure 1.1. Further assume that relations between all variables in the DAG are linear. With measures of \(X\), \(W\), \(Z\), and \(Y\) in hand, we estimate a linear regression model of this form:

\[ \text{Y} = \beta_1 + \beta_2 X + \beta_3 Z + \beta_4 W + \varepsilon \tag{1.1}\]

At first glance, it may seem that this model allows us to simultaneously estimate the effects of both \(X\) and \(Z\) on \(Y\). Unfortunately, the coefficients in Equation 1.1 do not have such a straightforward causal interpretation.

On the one hand, the model includes enough control variables to eliminate confounding with respect to \(X\).5 As a result, \(\hat{\beta}_2\) can be interpreted causally, as an estimate of the effect of \(X\) on \(Y\). On the other hand, Equation 1.1 includes control variables that are “post-treatment” with respect to \(Z\); the model adjusts for variables that lie downstream on the causal path between \(Z\) and \(Y\). Thus, \(\hat{\beta}_3\) should not be interpreted as capturing the total causal effect of \(Z\) on \(Y\).

This illustrates what Westreich and Greenland (2013) call the “Table 2 Fallacy”: Two similar-looking statistical quantities, estimated by a single regression model, can have very different substantive interpretations. More often than not, the coefficients associated with control variables in a regression model are incidental to the analysis. It is a mistake to interpret them individually, one after the other, as if they each captured a causal effect or correlation of interest. To avoid this trap, researchers must define their estimands explicitly, and only highlight the empirical quantities that actually answer their research questions.

If defining one’s estimands is so important, why do many researchers neglect to do so? Part of the explanation may simply be that statistical and causal inference are hard problems. It can often be difficult for researchers to follow a consistent thread through theory development, study design, measurement, and statistical modelling, all the way to estimates of our ultimate quantities of interest. To compound this challenge, the terminology used to describe those quantities is, frankly, a big mess. Indeed, many technical terms have parallel or outright contradictory meanings.

Consider the popular expression “marginal effect.” In some disciplines, like economics and political science, a marginal effect is defined as the slope of the outcome with respect to one the model’s predictors. In that context, the word “marginal” is meant to evoque the effect of a small change in one of the model’s predictors on the outcome. In contrast, when researchers in other disciplines write the words “marginal effect,” they typically signal that they are taking an “average” of unit-level effect estimates. In the former case, “marginal effect” refers to a derivative; in the latter, it refers to the process of marginalization, that is, to an integral. The same expression has two exactly opposite meanings!

To overcome terminological ambiguity, and to help researchers describe their quantities of interest more accurately, Chapter 3 introduces a simple yet powerful conceptual framework. By answering five simple questions, analysts will be able to clearly define their empirical estimands.

1.3 Making sense of parameter estimates

Consider a typical statistical setting where the analyst asks a research question, and selects a model to meet domain-specific requirements. Perhaps the model is designed to capture a salient feature of the data-generating process, achieve a satisfactory level of goodness-of-fit, or fulfill a conditional independence assumption for causal inference. The analyst fits their model using an estimator, and obtains parameter estimates along with standard errors.

Even if a fitted model is relatively simple, the parameter estimates it generates may not map directly onto an estimand that could inform one’s research question; the raw parameters may be very difficult to interpret substantively. For example, an analyst who fits a logistic regression model to a binary outcome will typically get coefficient estimates expressed as log odds ratios, that is, as the natural logarithm of a ratio-of-ratios-of-probabilities. Despite the simple nature of this model, its parameters are still expressed as complicated functions of probabilities.

But even the most straightforward probabilities are notoriously challenging to grasp intuitively. Indeed, a substantial body of literature in psychology and behavioral economics documents various biases that distort how individuals perceive and make decisions based on them. In their seminal work, Kahneman and Tversky (1979) argue that people tend to “underweight outcomes that are merely probable in comparison with outcomes that are obtained with certainty.” Numerous other biases have been identified over the years, including the “base rate fallacy” and various “conservative biases” (Nickerson 2004).

If understanding simple probabilities is already difficult, how can we expect colleagues and stakeholders to grok weird statistical constructs like odds ratios? How do we interpret the estimates produced by fancy regression models with splines and interactions? How can we help our audience understand the results produced by mixed-effects Bayesian models, or by complex machine learning algorithms?

The main contention of this book is that, in most cases, analysts should not focus on the raw parameters of their models. Instead, they should transform those parameters into quantities that make more intuitive sense, and that shed light directly onto their research question. Instead of reporting log odds ratios, analysts who fit logistic regressions should transform coefficients into predicted probabilities, and compare predictions made with different values of the right-hand side variables.

In Chapter 3, we will see that this particular transformation, from logit coefficients to predicted probabilities, is but one example of a much more general workflow. This workflow can be applied consistently, in model-agnostic fashion, to interpret the results of over 100 different classes of statistical and machine learning models.

  1. One way to buttress claims to causal identification is to argue that a model satisfies the “backdoor criterion” (Pearl 2009). A set of control variables \(\mathbf{K}\) fulfills this criterion relative to a pair of variables \((X,Y)\) if no node in \(\mathbf{K}\) is downstream in the causal path from the treatment \(X\); and if elements of \(\mathbf{K}\) “block” every path between \(X\) and \(Y\) that contains an arrow into \(X\). Morgan and Winship (2015) offer a good introduction to the backdoor criterion and to statistical adjustment strategies for blocking paths.↩︎

  2. Note that repeated measurements do not solve this problem, since a person is not exactly identical at times \(t\) and \(t+1\).↩︎

  3. Readers who need to know if their statistical results can be interpreted as causal estimates are encouraged to read one of the many excellent books published on the topic, e.g. Pearl (2009), Angrist and Pischke (2009), Morgan and Winship (2015), Imbens and Rubin (2015), Pearl and Mackenzie (2018), or Hernán and Robins (2020).↩︎

  4. TODO: Cite on overfitting↩︎

  5. In the language of Pearl and Mackenzie (2018) and Morgan and Winship (2015), the backdoors between \(X\) and \(Y\) are closed.↩︎